Implementing the Fibonacci Sequence in Python

The Fibonacci sequence is a classic mathematical sequence that is widely used in computer science and algorithm design; this article will introduce four methods of implementing the Fibonacci sequence using the Python programming language.

1. Recursive method

The recursive algorithm is the simplest way to implement the Fibonacci sequence. The code is as follows:

import time

def fibonacci_recursive(n):
    if n <= 1:
        return n
    else:
        return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)

n = 40
start = time.time()
value = fibonacci_recursive(n)
print(f"第 {n} 项为 {value}\n耗时: {time.time() - start}")

Program running results

第 40 项为 102334155
耗时: 26.679578065872192

Although the recursive algorithm is simple and easy to understand, its time complexity is relatively high O(2n), which is suitable for understanding the basic structure of the Fibonacci sequence.

2. Iterative method

The iterative method is more efficient and suitable for calculating the Fibonacci sequence in a larger range. The code is as follows:

import time

def fibonacci_iterative(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

n = 40
start = time.time()
value = fibonacci_iterative(n)
print(f"第 {n} 项为 {value}\n耗时: {time.time() - start}")

Program running results

第 40 项为 102334155
耗时: 0.0

This method is implemented through a loop, with a time complexity of O(n), which is more efficient than the recursive method.

3. Dynamic programming method

The dynamic programming method improves efficiency by storing the results of sub-problems, which is very suitable for calculating very large Fibonacci series. The code is as follows:

import time

def fibonacci_dynamic(n):
    fib = [0, 1]
    for i in range(2, n+1):
        fib.append(fib[i-1] + fib[i-2])
    return fib[n]

n = 40
start = time.time()
value = fibonacci_dynamic(n)
print(f"第 {n} 项为 {value}\n耗时: {time.time() - start}")

Program running results

第 40 项为 102334155
耗时: 0.0

This method also has a time complexity of O(n), but a space complexity of O(n), making it suitable for scenarios that require fast calculation results.

4. Use the general formula

The general formula for the Fibonacci sequence is:

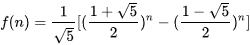
Use Python to implement as follows:

import time
import math

def fibonacci_form(n):
    sqrt5 = math.sqrt(5)
    phi = (1 + sqrt5) / 2
    psi = (1 - sqrt5) / 2
    return int((phi**n - psi**n) / sqrt5 + 0.5)

n = 40
start = time.time()
value = fibonacci_form(n)
print(f"第 {n} 项为 {value}\n耗时: {time.time() - start}")

The time complexity using the general formula is O(1).